Mange tenker at realfag er tørt og kjedelig. Kanskje spesielt matematikk er for mange bare tall og regneregler – ikke alle sine favoritting akkurat. Likevel er det ekstremt mye spennende vi kan fremstille, fortelle og vise ved hjelp av realfag og matematikk.
Her kan du lese et spennende eksperiment som vil forklare uendelighetsbegrepet på en litt artig måte. Hilberts Hotell er et paradox om et hypotetisk hotell laget av matematikeren David Hilbert.
Et fullt hotell med uendelig antall rom
Se for deg at du kommer inn på et hotell, men det er ikke et hvilket som helst hotell. Hotellet har uendelig med rom. Du står i resepsjonen og er klar for å sjekke inn, men det er bare ett problem: hotellet er fullt. Resepsjonisten er heldigvis smart og vet hvordan hun skal finnes et rom for deg.
Hun forteller gjestene i rom 1 at de må flytte seg til rom 2. Gjestene i rom 2 flytter seg til rom 3, osv. Vi kan si at gjesten i rom n flytter seg til rom n+1.
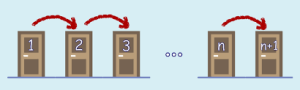
Se for deg at alle flytter rom samtidig. Da vil det være plass til deg på rom 1, og alle gjestene vil fremdeles ha et rom å bo på – nettopp fordi det er uendelig mange rom.
Dette eksperimentet viser at uendelig pluss 1, fremdeles er uendelig.
K antall gjester
Dette eksperimentet er spennende fordi vi kan endre antallet personer som trenger et rom til et absurd nummer, og det vil fremdeles være et korrekt. Se for deg at det ankommer k antall gjester på dette fullbookede hotellet med uendelig antall rom, og de ønsker deg k rom. Ikke noe problem! Den smarte resepsjonisten ber hver gjest på hotellet om å flytte seg k rom bortover gangen. Da vil de k gjestene kunne flytte inn på de k første rommene på hotellet.
Det vil si; hvis 3 personer ankommer vil resepsjonisten be dem i rom 1 om å flytte seg til rom 4, og de i rom 2 til å flytte seg til rom 5, og de i rom 379 flytte seg til rom 382. Gjestene kan da flytte inn på rom 1, 2 og 3.
Uendelig antall gjester
La oss ta eksperimentet ett steg videre! Hva om uendelig antall gjester ankommer hotellet og ønsker seg hvert sitt rom? Dette kan vi løse ved å flytte gjestene i rom 1 til rom 2, gjestene i rom 2 til rom 4, og gjestene i rom n til rom 2n. Det faktum at no
en av gjestene må flytte seg til rom ganske langt unna er ikke noe vi bryr oss om – vi er kun interessert i matematikken bak dette:-)
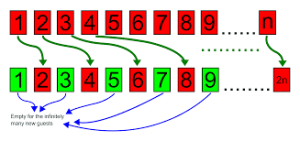
Legg merke til at når vi flytter gjestene fra rom n til rom 2n vil alle rommene med oddetalls-romnummer stå ledig – og vi kan enkelt plassere de uendelig mange gjestene i disse rommene.
Grunnen til at dette fungerer er fordi «størrelsen» (eller kardinaliteten) til settet av de naturlige tallene er den samme som kardinaliteten til settet av alle partallene.
Uendelig antall busser med uendelig antall pasassjerer
Som et siste eksempel kan du se for deg et uendelig antall busser, hvor hver buss inneholder et uendelig antall personer. Alle ankommer det fullbookede hotellet og ønsker hvert sitt rom. For vår smarte resepsjonist er det, igjen, ikke et problem!@

Hun sier at vi kan markere hver buss og hvert sete på bussen med et tall. Dermed vil hver person ha et unikt par bestående av to tall (s,b): s er setenummer og b er bussnummer. Vi kan og si at personene som allerede er på hotellet har b = 0. Dermed sier vår smarte resepsjonist at hun vil putte hver person i rom nummer 2^s * 3^b.
For eksempel personen i rom 1119744 = 2^9 * 3^7 satt på buss 7 på sete 9.
Dette trikset kalles primfaktorisering, og vi kan løse enda større problemer på denne metoden. Som for eksempel hva om et uendelig antall ferger alle hadde et uendelig antall busser som alle hadde et uendelig antall passasjerer?
Hilberts Hotell er bare ett av mange paradox og fenomen innenfor matematikken. Personlig syntes jeg det er kjempespennende å kunne tenke på denne måten, og ikke minst at det kan forklares med matematikk!

